

<< Előző oldal Következő oldal >>
A Koch-féle hópehely


<< Előző oldal Következő oldal >>
A Koch-féle hópehely
Helge von Koch svéd matematikus 1904-ben egy különös geometriai alakzatot írt le, amely nagy fejtörést okozott az akkori matematikus társadalomnak.
Induljunk ki egy egységnyi oldalú háromszögből!

Mindhárom oldalára állítsunk egy 1/3 oldalú háromszöget!

Ismét minden oldalra állítsunk egy harmad oldalú háromszöget!

Majd újra!

És így tovább a végtelenségig…
Mekkora a Koch-féle hópehely kerülete?
Az alábbi ábra alapján meghatározhatjuk a kerület számításának szabályát.
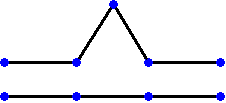
Láthatjuk, hogy az egyenes szakaszok hossza minden lépésben négyharmadszorosára nő.
Tehát a kerület képlete:
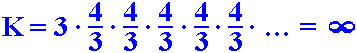
Mivel a képzési lépések száma végtelen, a kerület is végtelen nagy lesz.
(A képlet elején a hármas szám a kiindulási háromszög kerületét jelenti.)
Mekkora a Koch-féle hópehely területe?
Pontosan nem határozzuk meg a területet, de annyit megállapíthatunk,
hogy az alakzat a kezdő háromszög köré írt körön belül helyezkedik el,
így területe bizonyosan kisebb, mint a fent említett köré.
(Továbbá láthatjuk, hogy belül van a második ábra köré rajzolt hatszögön is.)
A Koch-féle hópehely egy véges területen elhelyezkedő végtelen hosszú görbét ír le. Így hosszúságban nem különbözik egy szintén végtelen (, az egész világegyetemet átszelő) eukledeszi egyenestől, viszont elfér akár az előttünk lévő monitor képernyőjén is. Sőt bármilyen kicsiny háromszögből is indulunk ki, minden esetben végtelen hosszúságú görbét kapunk eredményül. A Koch-féle hópehely az egyik legegyszerűbben leírható fraktál, amely minden szinten nagyszerűen mutatja az önhasonlóság tulajdonságát.

Tudomány és Technika (test@t-es-t.hu)
<< Előző oldal Vissza az oldal elejére Következő oldal >>

