<< Előző oldal    Következő oldal >>

 

Milyen hosszú a tengerpart?

Az angol Lewis F. Richardson a XX. század első felében a földrajzi határvonalak és országhatárok hosszának, illetve hosszmeghatározásának pontosságát vizsgálta. Észlelte ugyanis, hogy bizonyos országok közös határainak hossza egyes forrásokban nagy eltérésekkel szerepel. Átgondolva a dolgot, láthatjuk, hogy a partvonalak és országhatárok hosszának megállapítása többféleképpen történhet és eljárásonként más és más eredményeket kapunk. Az alábbi ábrán két módszert láthatunk, amelyekkel egy térképen határozhatjuk meg egy partvonal körülbelüli hosszát.

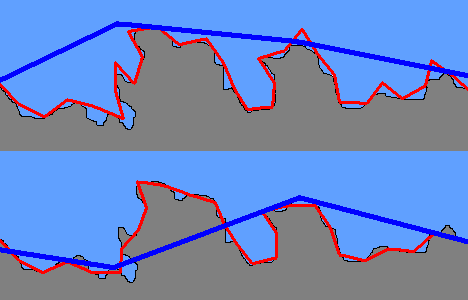
A ábra felső részén vonalzót, az alsó részén körzőt használva állapítjuk meg ugyanannak a partszakasznak a hosszát. Fent különböző hosszúságú vonalzókat illesztünk a partvonalhoz, alatta pedig különböző körzőnyílásokkal metszük el a partvonalat. A két eljárás különbözőségének jól látható voltán kívül megállapíthatjuk, hogy mindkét módszer esetében kisebb lépések alkalmazásakor (piros) nagyobb hosszúságot kapunk eredményül. Ez természetes, hiszen egy kisebb vonalzóval pontosabban követjük a partvonalat. Minél kisebb mérési egységet választunk, annál pontosabban kapjuk a partvonal hosszát, persze annál több munkával.

Benoit Mandelbrot ötven évvel később felhasználta és újraértelmezte a fenti problémát. Gondolatban próbáljuk meghatározni egy partvonal tényleges hosszát úgy, hogy egyre kisebb mérési egységet alkalmazunk. Ha egyméteres egységet választunk, nem vesszük figyelembe az egy méteresnél kisebb görbületeket, amelyek pedig a partvonal teljes hosszán végigvonulnak, így annak hosszát növelik. Ha tíz centiméteres egységgel mérünk, kihagyjuk a centiméteres görbületeket, és így tovább…

Ahogy egyre közelebbről vizsgáljuk a partvonalat, mindig felfedezhetünk újabb mintázatokat, amelyeket a mérésnél figyelembe kell vennünk.

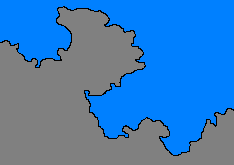
A gyakorlatban a partvonal pontos hosszát csak egy atomi szintű mérési egységgel tudjuk megmérni, hiszen a fenti önhasonlóság (mai tudásunk szerint) az atomi szintig folytatódik.

Mandelbrot egy a partvonalakhoz hasonló geometriai alakzatot képzelt el, amelynél az önhasonlóság a végtelen kis mérettartományokig folytatódik. Ebből következik, hogy egy ilyen alakzat körvonalának hossza végtelen, hiszen minden szinten találhatunk még finomabb görbületeket, üregeket és hajlatokat.

Mandelbrot, kutatásai során számos természet alkotta szerveződésben fedezte fel az ehhez hasonló felépítést. Majd 1975-ben elnevezte a fentihez hasonló geometriai alakzatokat fraktáloknak. (Angolul fractal, ami főnév és melléknév is. A név az angol fracture szóból származik, melynek jelentése: törés.) Ez az elnevezés a Káosz-elmélet egyik alapszava lett, a fraktálgeometria pedig felsorakozott a geometria résztudományai közé.

  Tudomány és Technika (test@t-es-t.hu)

<< Előző oldal    Vissza az oldal elejére    Következő oldal >>