

<< Előző oldal Következő oldal >>
A Cantor-halmaz


<< Előző oldal Következő oldal >>
A Cantor-halmaz
Benoit Mandelbrot a Káosz-elmélet egyik megalkotója. Munkássága során feltárta a természetes alakzatok (sziklák, növények, az élő szervezetek belső felépítése, stb.) felépülésének kaotikus voltát. Felfedezett egy geometriai alakzatot, amellyel jól szemléltethetjük a természetes kaotikus rendszerek tulajdonságait (, amelyet ezért Mandelbrot-halmaznak nevezünk).
Mandelbrot az 1960-as évek elején az IBM cégnél végzett kutatásokat, ekkor vizsgálta meg a világszerte jól dokumentált gyapotár változások ütemét. A gyapotár-változások magyarázata ugyanis sok gondot okozott a közgazdászoknak, mivel azok nem igazolták az akkoriban elfogadott elméleteket. Mandelbrot minden hozzáférhető adatot beszerzett egészen a napi árváltozások szintjéig.
Ezen vizsgálatok vezettek el a kaotikus folyamatok egyik fő tulajdonságának felismeréséhez. Mandelbrot a különböző (napi, havi, éves) időintervallumok grafikus ábrázolása után azt tapasztalta, hogy a napi görbe jellegét és mintázatát tekintve szinte azonos a nagyobb időszakok görbéivel. Tehát a görbe az egyes mérettartományokban nagyon hasonló:
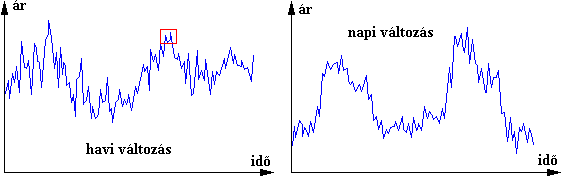
(Ez nem Mandelbrot ábrája. Az ábra célja csak a szemléltetés,
így nem valós adatok vannak ábrázolva.)
Mandelbrot ezt a tulajdonságot a mérettartományok szimmetriája miatt skálázásnak nevezte. Vagyis más és más osztású skálákat választva vizsgálatainkhoz, közel megegyező görbéket kaphatunk, ha az osztás értékét jól választjuk meg. A "skálázás" szó egyik legközelebbi szinonímája az önhasonlóság, amely a magyar nyelvben sokkal pontosabban utal a jelentésre.
Mandelbrot, vizsgálatai során más gazdasági folyamatok esetén is felfedezte ezt a tulajdonságot. Most viszont említsük meg egy műszaki problémával kapcsolatos kutatását!
Az IBM cég mérnökeinek is gondot okozott a zajos vezetékes telefonvonalakon keresztüli adatátvitel. (Ahol valójában számítógépek kommunikációjáról volt szó, mint például manapság az otthoni Internet-kapcsolat analóg vonalon keresztül.) Az előforduló átviteli hibákat a jel erősítésével próbálták csökkenteni, ugyanis erősebb jeleket a zaj csak kevésbé tud elnyomni. Azt tapasztalták, hogy a hibákat nem tudják kiküszöbölni, legfeljebb csökkenteni a számukat. Hosszú hibamentes időszakok után mindig előfordult néhány hiba, furcsa időbeli elrendeződéssel.
Mandelbrot meghallgatva a szakemberek tapasztalatait és vizsgálva a rendelkezésre álló mérési eredményeket felállított egy matematikai modellt, amely közelítőleg helyesen írta le a hibák időbeli eloszlását. Amely tulajdonképpen megegyezett egy XIX. századi matematikus, Georg Cantor által már megadott számhalmazzal. Ezt a halmazt Cantor-halmaznak nevezik, amelyet legkönnyebben képzési szabályának megadásával tudunk megadni.

Vegyünk alapul egy szakaszt, amely esetünkben egy időtartamot jelöl. Távolítsuk el a szakasz középső harmadát, majd az így kapott szakaszok középső harmadát és így tovább a végtelenségig. (A fenti ábrán csak az első hat lépés van ábrázolva.)
Ezt az elvet követve, eredményül végtelen sok szakaszt kapunk, amelyek összesített hossza nulla. A gyakorlatban a felbontást a jelek küldési időközéig kell folytatnunk. (Manapság ez egy telefonvonalon kb. 20 ms-os időközöket jelenthet.) Ha megvizsgáljuk az adatátvitel egyik nagyobb hibás időszakát, mindig találunk benne hibátlan tartományokat, és így tovább a kisebb időtartományok felé haladva. Ez a hibaelrendezés feltételezi a hibák elkerülhetetlenségét, így a műszaki fejlesztést más irányba tereli. Nem a hibátlan adatátvitelen kell fáradozni, hanem az adatokat hibafelismerési vagy hibajavító kódokkal kell kiegészíteni, amelyek segítségével a létrejövő hibák ellenére is biztosítható a hibátlan kommunikáció.
(A matematikai pontossággal előállított Cantor-halmaz valójában nem is ábrázolható, hiszen az egyes szakaszok hossza nulla, és számuk végtelen. Ezért ezt a halmazt Cantor-pornak is nevezik.)
Megvizsgálva a fenti ábrát, felfedezhetjük a halmaz mérettartományainak szimmetriáját, vagyis az önhasonlóság tulajdonságát.
Tudomány és Technika (test@t-es-t.hu)
<< Előző oldal Vissza az oldal elejére Következő oldal >>

