<< Előző oldal    Következő oldal >>

 

A csöpögő vízcsap

Menjünk oda egy hagyományos vízcsaphoz! Finoman kezdjük el kinyitni, amíg lassan csöpögni nem kezd! Tovább nyitva a csapot a csöpögés gyorsul, illetve a cseppek lehullása közötti idő csökken.

Azt hinnénk, hogy további nyitás hatására az egyre gyorsuló periodikus csöpögés egyenletes átmenettel folyamatos vízoszloppá változik. Vagy vannak más tapasztalataink? Lassan tovább nyitva a csapot, azt látjuk, hogy a a vízcseppek már nem azonos időközönként esnek le, hanem kettesével. Ez bizony egy mindenki által könnyen demonstrálható valódi bifurkáció. (Egy modern egykaros keverős vagy szűrőbetétes vízcsappal esetleg nagyon nehéz lehet ezt elérni, mert nem szabályozható elég finoman a kifolyó vízmennyiség.)

Nehezebben megfigyelhető, hogy további nyitásra már négy különböző követési idővel esnek le a cseppek. Majd elérhetjük a teljes összevisszaság állapotát, amikor nem találunk szabályszerűséget. A cseppek kaotikus szabálytalansággal követik egymást.

Robert Shaw felállított egy mérőrendszert a csöpögő vízcsap vizsgálatára. Egy állandó vízszintű tartállyal biztosította az állandó víznyomást. A cseppek követési idejét mérte és regisztrálta különböző csapbeállítások (átfolyó vízmennyiség) mellett. A jelenséget matematikailag is modellezte. A modellje nagyon jó közelítéssel fedte a valós mérési eredményeket, így lehetőséget adott további számításokra, olyan tartományokban, amelyek már mérhetetlennek bizonyultak.

Shaw mérési és számítási eredményeit a következő módszerrel ábrázolta. Egy derékszögű koordinátarendszerben pontokat ábrázolt. Egy pontot három egymás után lehulló vízcsepp két időközének ábrázolásával kapott. Az x tengelyre felmérte az első két vízcsepp leesése közötti időt, amihez az y tengely irányában a második és harmadik vízcsepp lehullása közötti időt társította. Így szemléletessé váltak a mérés és számítás során kapott számsorok.

Egyenletes csöpögés ábrázolása Shaw szerint:

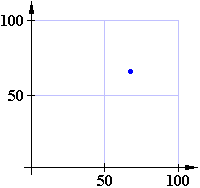
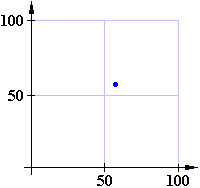
Az első ábrán 70ms-os, a másodikon 60ms-os időközökkel követik egymást a cseppek.

Az első bifurkáció után, amikor a követési időközök például: 50ms, 80ms, 50ms, 80ms, stb…

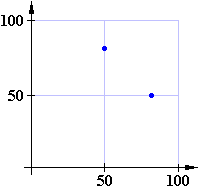
A következő bifurkáció után (38ms, 83ms, 50ms, 87ms) (x1 = 0,4; r = 3.5):

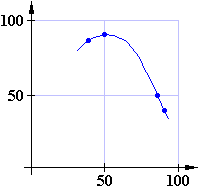
Néhány bonyolultabb ábra az ökológiai szimulációs program alapján:

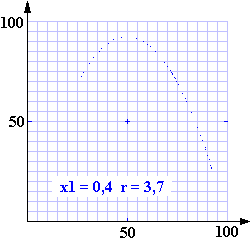
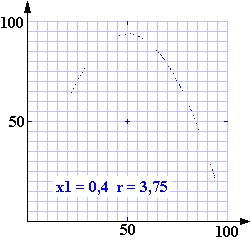
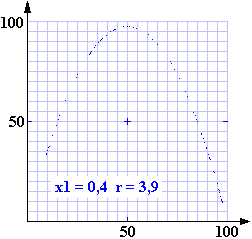
Láthatjuk, hogy az ábrákon a pontok egy jól kivehető görbe mentén helyezkednek el. Az egymáshoz közeli pontok időben nagyon távol is állhatnak egymástól. Ne felejtsük el, hogy a görbéket egy véletlenszerűnek tűnő számsorból kapjuk. A fenti ábrák után már el sem titkolható, hogy a szimulációs programban a parabola egyenletét használtuk fel.

A Káosz-elmélet kutatói a fentieknél bonyolultabb háromdimenziós ábrákat is használnak, amelyeknél egy pont helyét három egymást követő számból nyerik a fentiekhez hasonlóan. Így még több geometriai információ is nyerhető egy kaotikus számsorból (mérési eredményből).

Hogy egy kaotikus számsor miben különbözik egy véletlenszerű számsortól, azt a következő véletlenszám-generátorral előállított ábrából láthatjuk:

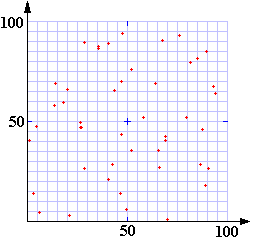
Tehát, a kaotikus rendezetlenség nem egyenlő a véletlenszerű rendezetlenséggel.

  Tudomány és Technika (test@t-es-t.hu)

<< Előző oldal    Vissza az oldal elejére    Következő oldal >>