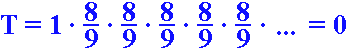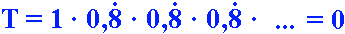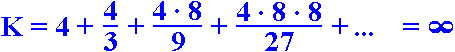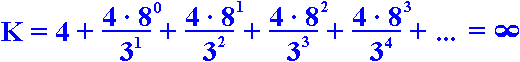<< Előző oldal
Következő oldal >>
Sierpiński-szőnyeg, Menger-szivacs
Érdemes megismerkedni ezzel a két nagyon szemléletes
fraktállal, amelyek egyszerűen képezhetők!
A Sierpiński-szőnyeg előállításánál egy négyzetből indulunk
ki, aminek eltávolítjuk a középső kilenced részét. Majd a maradék nyolc
kilenced résznek is eltávolítjuk a közepét, és így tovább… a végtelenségig:

Mekkora a szőnyeg területe?
A kiindulási négyzet oldalát tekintsük egységnyinek, tehát a kiindulási négyzet területe is
egységnyi.
Minden lépésben eltávolítjuk az előző síkidom egykilenced részét,
vagyis a terület minden lépésben nyolckilencedszeresére változik, azaz csökken.
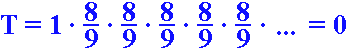
Tizedestörtekkel:
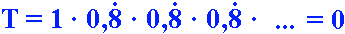
Mekkora a szőnyeg kerülete?
Vagyis mekkora a síkidom határolóvonalainak összege?
A fenti ábra alapján a következő képletet írhatjuk fel:
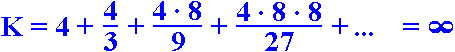
,amelyből általánosabban:
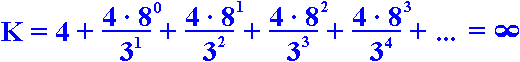
Tizedestörtekkel szorzat alakban:

Mindezek alapján elmondhatjuk, hogy ez a szőnyeg egy
különleges síkidom, amely egy adott területen belül helyezkedik el, mégis
végtelen hosszú a határológörbéje, a területe viszont nulla. A fenti szőnyeg és
még több hozzá hasonló idom és alakzat már a huszadik század elején
megszületett néhány leleményes matematikus gondolatában. Ezek sok fejtörést
okoztak az akkori felfedezőknek. Vajon hová is sorolható be egy ilyen terület
nélküli idom, ami több, mint egyenes, de mégis kevesebb, mint egy síkidom? Így
született meg a tört dimenzió fogalma. Fél évszázaddal később Benoit Mandelbrot
ezeket az eredményeket használta fel a fraktáldimenzió megfogalmazására, amely
a fraktálok egy jellemző alaptulajdonsága. (Az euklideszi geometriában az
egyenesek egydimenziós, a síkidomok kétdimenziós, a testek háromdimenziós
kiterjedésűek.)

A Sierpiński-szőnyeg háromdimenziós
megfelelője a Menger-szivacs:

A szivacs élhossza és felszíne végtelen, térfogata viszont nulla.
A Menger-szivacs egy másik formája:

Peter Wonka
szíves engedélyével
Tudomány és Technika
(test@t-es-t.hu)
<< Előző oldal
Vissza az oldal elejére
Következő oldal >>