<< Az előző oldal   Tartalomjegyzék   A következő oldal >>

Fejlesztés alatt!

Számok, számrendszerek
A 10-es számrendszer története

Számok, számrendszerek

      A gondolkodó ember történetének őskorában, a törzsi együttélés, a közös munka (eszközkészítés, vadászat, gyűjtögetés; később földművelés, állattenyésztés) velejárójaként, a beszélt nyelvvel együtt lassan kialakultak a számok (természetes számok) nyelvi alakjai is. A nyelv, igény szerint bővülve, egyre nagyobb számok közlését tette lehetővé, de egy bizonyos számosság fölött már értelmetlen minden számra külön nevet alkalmazni. A nagyobb számok kifejezése bizonyosan valamilyen számrendszer alkalmazásával történt. Például: 10 alapszám (1-től 10-ig külön szóval jelölve), ami egy "csapat"-ot jelent (egy csapat = 10 darab), így alkalmas a 10 "csapat"-ig, 100-ig (hét csapat és még négy = 74), illetve akár 10-szer 10 "csapat"-ig, 1000-ig történő számolásra is (háromszor tíz és még kettő csapat = 320). Ez a 10-es számrendszer alkalmazása, amelynek első ismert megjelenése az i. e. 4000 körüli Elámból származik. Természetesen a társadalom és gazdaság fejlődésével szükségessé vált a számok írásos rögzítése is, kialakultak a számok és "csapatok" jelölésére használt számjegyek. Szintén természetes, hogy a (viszonylag elszigetelt) népcsoportok, ahogyan más nyelvet, úgy más számrendszert, más számjegyeket használtak.
      Az írott történelem bizonyítja, hogy az ókorban az ember ujjainak számából következő 10-es számrendszeren kívül még több, elvileg egyenértékű, de kissé körülményesebb számrendszert is alkalmaztak. (Az 5-ös számrendszert, amely az egy kézen levő ujjak számából ered még a 20. században is használták egyes afrikai törzsek. A 6-os számrendszert használták Pápua Új-Guineán. Az ujjközök számából eredő 8-as számrendszert használták egyes Észak-Amerikában élő törzsek. Az egy kéz hüvelykujjal számolható ujjperceinek számából eredő 12-es számrendszer használatára utalnak az egyes nyelvekben külön szóként megjelenő 11 és 12 számok, a tucat fogalom használata, az órák és a hónapok felosztásai. Egészen 1959-ig hivatalosan is jelen volt a hagyományos 16-os számrendszer használata a kínai súlyméréseknél. A 20-as számrendszert használta számos törzs és nemzet Afrikában, Dél-Amerikában, Ázsiában, és számos európai nyelvemlék is bizonyítja annak korábbi jelenlétét. A 60-as számrendszer használata már az i. e. 3000 körüli sumér leleteken is megfigyelhető, de ennek maradványa a 60 perces órák, a 60 másodperces percek és a szögek, szögpercek, szögmásodpercek hagyományos alkalmazása is.)
      A különböző kultúrákban használt számábrázolás sokszor vegyes, több számrendszert is alkalmazó volt, illetve különböző feladatokra (például darabszámra és súlymérésre) más és más számrendszert használt.
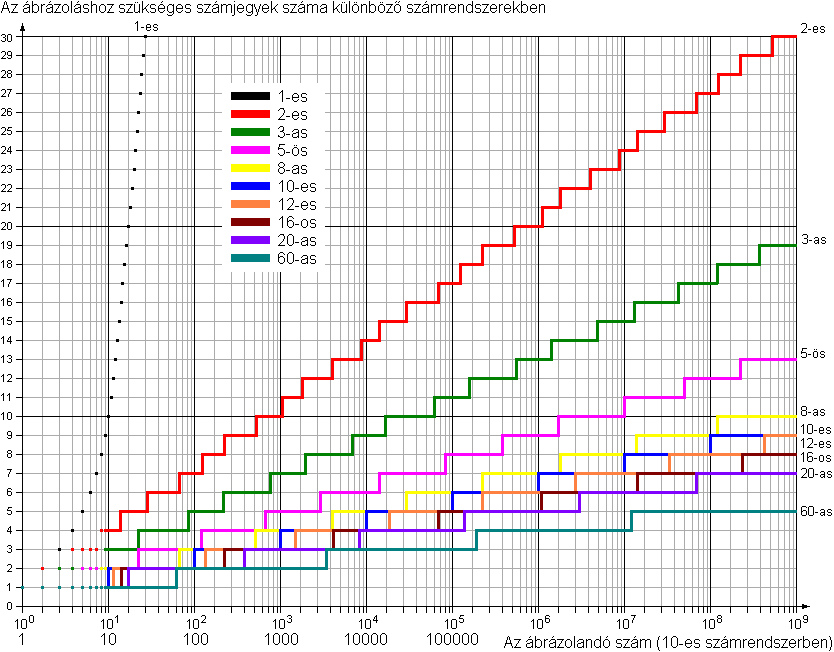
      A következő ábra a fent említett egyes számrendszerek tulajdonságait mutatja be, a ma is használt, tisztán helyiértékes számábrázolás esetén. A vízszintes tengelyen a leírni kívánt pozitív egész szám van feltüntetve, a függőlegesen az ehhez szükséges számjegyek száma. (A grafikon természetesen nem folytonos, hanem vízszintes vonalakon elhelyezkedő pontokból áll, de a szemléletesség kedvéért 10 fölött, ahol a pontok amúgy is vonalakká folynak össze, már folytonosan van ábrázolva, a számjegyek közti átmenet függőleges összekötéseivel. A nagyobb alapszámú számrendszer grafikonja takarja a kisebbet, de az átmenetek ábrázolása megmutatja a takart grafikonok valós méreteit.)

      Melyik az ember számára ideális számrendszer?
      Természetesen, egy bizonyos szám bármelyik számrendszerben ábrázolható, és a különböző ábrázolások jelentés és pontosság tekintetében egymással teljesen egyenértékűek. A különbség a számok ember által való (minél könnyebb) értelmezhetőségében, az azokkal lehetséges műveletvégzésben (ami annál jobb, minél egyszerűbb) van.
      A fenti ábrán is látható, hogy minél kisebb egy számrendszer alapszáma, annál több számjegy szükséges egy adott mennyiség leírására, illetve fordítva, minél nagyobb az alapszám, annál kevesebb számjegyre van szükség. Látható, hogy a tízes számrendszerben négyjegyű 1000-es szám leírására kettes számrendszerben 10, hatvanas számrendszerben csak 2 számjegy szükséges. Ez a jellemző a nagyobb alapszámú számrendszereket helyezi előtérbe.
      Egy adott számrendszerben az alapszámnak megfelelő számú különböző írásjel (számjegy) szükséges a számok leírására. A kettes számrendszerben kettő (0 és 1), a tízesben tíz (0, 1, 2, 3, 4, 5, 6, 7, 8, 9), a tizenhatosban tizenhat (0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F), a hatvanasban hatvan (0, 1, 2, 3, 4..., sajnos nincs is ennyi betű a billentyűzeten). A kisebb alapszámú számrendszerekhez kevesebb számjegyre van szükség, kevesebb a betűkön kívüli külön írásjegy, (kevesebb szám-nyomógomb szükséges a billentyűzeteken) és sokkal kisebbek a szorzótáblák.
      Bizonyos, hogy itt is az arany középút lesz a megoldás, hiszen tudjuk, hogy a köznapi- és a tudományos életben a tízes számrendszer van használatban. Viszont, ha jobban belegondolunk, és ez már kevéssé ismert dolog, manapság, a számítógépek korában, a legtöbb számítási művelet kettes számrendszerben kerül elvégzésre és esetleg csak az eredmény kerül kijelzésre tízes számrendszerben. Valójában, egy adott idő alatt a Földön tízes számrendszerben elvégzett matematikai műveletek száma elenyészően kicsi a kettes számrendszerben elvégzettekhez képest, hiszen minden egyes személyi számítógép műveletek (melyek közül sok számolási művelet) millióit hajtja végre másodpercenként.
      A 8-as, 10-es, 12-es és 16-os számrendszerek előnyeiről, hátrányairól manapság is sok vita folyik a tudományos életben. A 8-as, 12-es és 16-os számrendszereknek léteznek jó értelemben vett "fanatikus" követői is, akik egy hivatalos számrendszerváltást is szeretnének elérni. (Octomatics: szemléletes számok nyolcas számrendszerben, Dozenal Society of America, The Dozenal Society of Great Britain, Hex Headquarters.)
     
     
      Melyik az a számrendszer, amely a legtömörebben tárolja az információt? (Vagyis minél kevesebb számjeggyel, minél rövidebben.)
      Az alábbi ábra a számrendszerek fent leírt két ellentétes jellemzőjét veti össze. angol írás

      A számolást, a számábrázolást, a számokkal való műveleteket különösen megnehezítették az ősi, kezdetleges számírási szabályok, a nulla számjegy hiánya, valamint a különböző számrendszerek (akár vegyes) használata.
      Egy nagyobb természetes szám leírása még a viszonylag új római számokkal is nehéz, de a bonyolultabb műveletvégzés (szorzás, osztás) szinte lehetetlen. Az ősi kultúrák hétköznapi gazdasági számítási feladataiban természetesen nem volt szükség nagy számokra és ezek összeadását és kivonását fejben el lehetett végezni. A modern számábrázolás helyiértékes rendszerű, nulla számjegyet is tartalmaz, így könnyű a nagy számok leírása és a műveletvégzés, valamint megvalósítható a tört számok ábrázolása is.
      méréstörténeti könyv
     

Vissza a lap tetejére

A 10-es számrendszer története

      a 10-es számrendszer használata
      i.e. 4000 Elám
      i.e. 3000 egyiptomi hieroglifák
      i.e. 2500 Babiloni számírás
      i.e. 1800-tól a görög kultúrában
      i.e. 1600 krétai hieroglifák, hettita hieroglifák
      i.e. 1000 kína
      i.e. ~500 india: nullát is tartalmazó decimális helyiértékes rendszer (628-ban Brahmagupta) Hindu–arab számírás
      i.sz. 1000 arab tizedestörtek
      Fibonacci, Robert Chester és/vagy Adelard of Bath lefordította l-Hvárizmi (angolul: Al-Khwarizmi) matematikai munkáit, amivel európában bemutatta a nullát is tartalmazó decimális helyiértékes rendszert, tizedestörtekkel

      1585: Simon Stevin: decimális rendszer
      Írása
     
     

      Christian Hughens: természeti állandók
     
     
     

      1739: Nicolas Louis de Lacaille és Jacques Cassini
      Jean Picard és Ole Römer
      Charles Maurice Talleyrand-Périgord: másodpercinga hossza
     

      1793: méter szó
      délkör kimérése
      1795: Marc Etienne Janety: 4db ősméter, 4db őskilogramm
      1799: 1db levéltári méter és 1db levéltári kilogramm

      1812: Napóleon rendeletei
      1832: Gauss mértékrendszer tanulmánya
      1837: újra hatályos
      1859: James Clark Maxwell javaslata a méter meghatározására
      1867: párizsi világkiállítás
      1872: Nemzetközi Méterbizottság

      1874: új méteretalonok készítése
     
     
     

Vissza a lap tetejére

  Tudomány és Technika (test@t-es-t.hu)

<< Az előző oldal   Tartalomjegyzék   A következő oldal >>