

<< Előző oldal Következő oldal >>
A Lorenz-féle vízikerék


<< Előző oldal Következő oldal >>
A Lorenz-féle vízikerék
Lorenz az időjáráshoz hasonló viselkedésű, úgynevezett kaotikus rendszerek után kutatott. Felfedezett egy érdekes mechanikai rendszert, amelynek viselkedése nagyon különös.
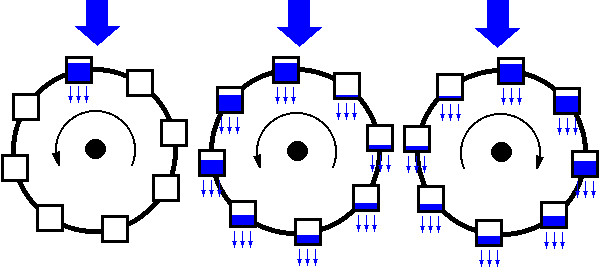
A folyadék a kerék tengelye felett ömlik egyenletesen a kerékre, így mindig az éppen felül levő edény töltődik. Az edények alján a folyadék egy a beömléshez képest kis keresztmetszeten kiürülhet. (Tekintsük úgy, hogy az edények alján kifolyó folyadék nem kerül bele az alatta levő edényekbe.)
Ha a folyadék lassan ömlik be, az edény kiürülése miatt nem keletkezik elegendő hajtónyomaték a kerék megindulásához.
Növelve a beömlés mennyiségét a felső edény annyira megtelik, hogy megindul a forgás, amely állandósulhat is bizonyos beömlési sebességek esetén.
Tovább növelve a beömlést, a kerék forgási sebessége elérhet egy akkora értéket, amelynél már nincs elég idő az edények kiürüléséhez és a forgás szabálytalanná, kaotikussá válik, a forgásirány is többször megfordul. A kerék szögsebessége az idő függvényében:
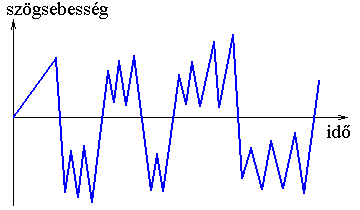
(A vízikerék mozgását Lorenznek sikerült leírnia egy viszonylag egyszerű egyenletrendszerrel:
dx/dt = 10(y-x)
dy/dt = –xz + 28x – y
dz/dt = xy – (8/3)z
Ezek az egyenletek úgynevezett differenciálegyenletek, amelyek a felsőoktatásban kerülnek tárgyalásra.)
Így lehetővé vált a rendszer számítógépes szimulációja, amely érdekes eredményt hozott. Lorenz a megoldásként kapott számhármasokat egy háromdimenziós koordinátarendszerben ábrázolta:

A fent láthatóhoz hasonló, különös határozott képet kapta, amelyből világosan kitűnt, hogy a kaotikus mozgás tartalmaz valamiféle rendet.
"Mindig határok között maradt, sosem futott ki a lapról, mégsem ismételte önmagát."
A fenti egyenletrendszer paramétereit változtatva különféle grafikus eredményeket kapunk, amelyek valamiféleképpen hasonlóak a fenti ábrához. Néhány további látványos példát tekinthetünk meg ITT (364kB).
Egy Lorenz függvényét megjelenítő animáció.
Tudomány és Technika (test@t-es-t.hu)
<< Előző oldal Vissza az oldal elejére Következő oldal >>

