Következő oldal >>

 

Pillangó-hatás = érzékenység a kezdőfeltételekre

A Massachusettsi Műszaki Egyetem (MIT) egyik meteorológiai kutatója, Edward Lorenz, 1960-ban készített egy időjárás szimulációs programot. Sikerült kiválasztania, meghatároznia néhány szabályt, amelynek követésével a számítógép-program élethűen szimulálta egy képzelt bolygó időjárását. A szabályok (egyenletek) a hőmérséklet és a nyomás, a nyomás és a szélsebesség viszonyát írták le.

A számítógép egy kezdeti feltételből (egy számsorból) kiindulva rövid idő alatt végigkövette akár egy egész nap időjárását is, és a kért időpontnak megfelelő helyzetet papírra nyomtatta. Ez a program nagyon egyszerűsített formában utánozta az időjárást, de a kinyomtatott eredmény, a szelek és hőmérsékletek változása mégis a földi időjáráshoz volt hasonló a maga változékonyságával és megjósolhatatlanságával.

A számítógép program nagyon fontos tulajdonsága, hogy ugyanazokra a kezdeti feltételekre mindig ugyanazokat az eredményeket adja (hacsak nem alkalmazunk véletlenszám generátort, de itt erről nem volt szó).

1961 telének egyik napján Lorenz egy régebbi programfutás utolsó időszakát szerette volna újra megvizsgálni. Megtehette volna, hogy a gondosan dokumentált kezdeti feltételekből megadja azt, amelyik végeredményére kíváncsi volt, de így végig kellett volna várnia a program teljes lefutásának hosszú idejét. Ezért inkább betáplált egy papíron meglévő részeredményt, amelyet a program az adott kezdeti feltétel futtatásának vége felé nyomtatott ki még az előző alkalommal.

(Mivel a számítógép minden további adatot az előzőből számol, így az adathalmaz egymásra épül. Tehát bármely pontban is indítjuk programunkat, (bármely már lejegyzett kezdőfeltétellel,) mindig ugyanazt az eredményt kell kapnunk.)

Lorenz a betáplált köztes eredményekkel elindította programját. A futás során azonban különös dolgot tapasztalt, a program eredményei egyre jobban eltértek az előző futás eredményeitől.

Hamar rájött, hogy a betáplált számokkal volt a baj, a számítógépe ugyanis hat tizedesjegyig számolt (0,134724), viszont helytakarékosság miatt csak három tizedesjegyig nyomtatták ki az eredményt (0,134). Így a visszatáplált számok valójában – mégha csak oly kis mértékben is, de – más kezdeti feltételt adtak meg.

Azt gondolnánk, hogy ez a kis eltérés nem okoz számottevő hibát, pedig itt az egy ezrelékes eltérés azt jelentette, hogy egy idő múlva már semmilyen hasonlóság sem volt a két futási eredmény között. (Gondoljunk bele, hogy mivel a hőmérséklet- és nyomásmérés hibája jóval nagyobb, mint egy ezrelék, akkor ez már magában lehetetlenné teszi a hosszútávú időjáráselőrejelzéseket.)

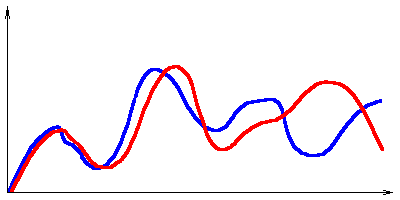
Lorenz ezekután nekilátott a probléma vizsgálatának ebből a szemszögből is. Rájött, hogy az időjárást és az ehhez hasonló viselkedésű folyamatokat olyan (nem lineáris) egyenletek írják le, amelyek nem oldhatók meg, legfeljebb közelítő módszerekkel a kívánt pontossággal számíthatók. Az ilyen rendszerekben bármilyen csekély bevitt hiba is teljes és átfogó hatással van a rendszerre. Tehát például az időjárási problémával folytatva, egy apró kis légáramlat, amelyet egy pillangó kelt a szárnyával, idővel óriási hatással van az időjárás egészére. Vajon földi létünk egyetlen másodperce alatt hány ilyen aprócska és nagyobbacska hatás éri légkörünket? Ha ezt figyelembe vesszük, bátran kijelenthetjük, hogy az időjárás egy "megjósolhatatlan" folyamat.

A fenti tulajdonság az ilyen (bizonytalan kimenetelű) rendszerek érzékenysége a kezdőfeltételre. A mondás szerint: "ha egy pillangó szárnya rebbenésével megmozdítja a levegőt Pekingben, akkor abból esetleg egy hónap múlva New Yorkban hatalmas viharrendszer támadhat."

Ez a szemlélet nem idegen az emberi gondolkodástól. Bizonyos hasonló feltevések már a népköltészetben is előfordultak:

Régen vitatott kérdés, hogy egyes emberi tettek válhatnak-e meghatározóvá történelmi méretekben? (A Káosz-elmélet szerint igen. A gazdasági és társadalmi folyamatok is az időjáráshoz hasonlóan viselkednek?)

Miért is fontos még Lorenz felfedezése? Bebizonyosodott tehát, hogy egyszerű köznapi formulákkal lehetséges nagyon bonyolult viselkedésű folyamatok leírása.

  Tudomány és Technika (test@t-es-t.hu)

Vissza az oldal elejére    Következő oldal >>