 Aktivitás
Aktivitás  Activity
Activity  Die Aktivität
Die Aktivität
| Tudomány és Technika | Természettudományok | Atomok és elemek |
Aktivitás - Radioaktív sugárforrás aktivitása
 Aktivitás
Aktivitás  Activity
Activity  Die Aktivität
Die Aktivität
Aktivitás fogalma
Fajlagos aktivitás, aktivitáskoncentráció
Bomlásállandó
Felezési idő
Bomlástörvény a felezési idővel kifejezve
Bomlástörvény a bomlásállandóval kifejezve
A bomlásállandó és a felezési idő összefüggése
Az aktivitás a radioaktív anyagok egy adott halmazában időegység alatt bekövetkező bomlások száma. A radioaktív anyagok (sugárforrások) aktivitása fokozatosan csökken.
Az aktivitás jele: A.
Az aktivitás SI mértékegysége: Bq (becquerel; 1/s).
1980-tól már (törvényesen) nem használható mértékegység: Ci vagy C (curie; 1 Ci = 3,7 · 1010 Bq).
1 Bq az aktivitása annak az elszigetelt rendszerként vizsgált anyaghalmaznak (tömegétől és térfogatától függetlenül), amelyben másodpercenként egy atommag bomlik szét.
Az aktivitás definíciójából adódó számítási összefüggés:
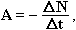
ahol ΔN a bomlásra képes atommagok számának Δt idő alatt történő megváltozása. Ez az összefüggés csak nagyszámú radioaktív atom relatív kicsiny időközönként történő vizsgálatakor érvényes.
Pontosabban:
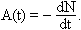
(Az összefüggés negatív előjele a bomlásra képes atommagok számának, így az aktivitásnak az időben való csökkenését fejezi ki.)
Fajlagos aktivitás: egységnyi tömegű anyag aktivitása.
A fajlagos aktivitás mértékegysége: Bq/kg.
Aktivitáskoncentráció (térfogati aktivitás): egységnyi térfogatú anyag aktivitása.
Az aktivitáskoncentráció mértékegysége: Bq/m3.
Egy radioaktív forrás aktivitása egyenesen arányos a bomlásra képes atommagjainak N számával:
A = λ · N, illetve A(t) = λ · N(t),
ahol λ a sugárforrás bomlásállandója [1/s]. A bomlásállandó az adott radioaktív anyagra jellemző konstans, amely az anyag egyetlen bomlásra képes atommagjának 1 s-ra vonatkoztatott bomlási valószínűségét adja meg (vagyis azt, hogy mennyi az esélye annak, hogy egyetlen mag egy másodperc alatt elbomlik).
Mivel N minden egyes bomlással csökken, az aktivitás is ezzel arányosan csökken. (Természetesen ezzel együtt a fajlagos aktivitás is folyamatosan csökken.)
A tapasztalat szerint bármely sugárforrás aktivitását állandó időközönként vizsgálva az aktivitás minden esetben ugyanolyan hányaddal (mértani sorozatként) csökken. (Például: ha az aktivitás bizonyos időtartam alatt feleződik, akkor a következő, pontosan akkora időtartam múlva is feleződik, és így tovább a teljes elbomlásig.)
A következő diagram egy tetszőleges radioaktív anyagban levő bomlásra képes atommagok számának változását mutatja be.
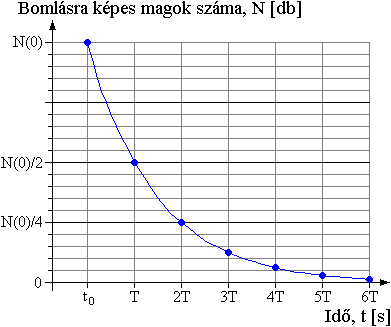
Látható, hogy T időtartam alatt a bomlásra képes magok száma feleződik. A T, az egyes radioaktív anyagokra jellemző állandó, a felezési idő. A radioaktív atommagok felezési ideje a 10-16 s-tól a 1015 évig terjedő tartományban található, amelyek elvi határoknak is tekinthetők, mivel a legalacsonyabb tartományokban már felmerülhet a létezés kérdésessége, a legmagasabb tartományok esetében viszont értelmetlenné válik egy, a világegyetem életkorához mérhető felezési idő megadása. (A világegyetem életkorához mérhető felezési idejű atommagok már stabilnak tekinthetők.)
A felezési idő fogalmának felhasználásával felírható a következő egyenletsor:
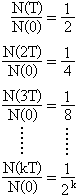
Az utolsó összefüggésből számítható a bomlásra képes magok számának pillanatnyi értéke a felezési idővel kifejezett időtartamok esetére. A k tényező az eltelt időtartam és a felezési idő közötti arányossági tényező (k = t / T).
Az összefüggés átalakítása a k = t / T helyettesítéssel:
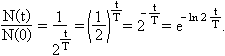
Átrendezés után:

amely összefüggés az exponenciális bomlástörvény.
Mivel az aktivitás (A) egyenesen arányos az anyaghalmaz bomlásra képes atommagjainak számával (N), az aktivitás változására is érvényes a fenti összefüggés:
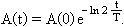
A bomlástörvény bomlásállandóval kifejezett alakja felírható az aktivitás bomlásállandóval kifejezett, valamint definíció szerinti alakjának összevetésével:
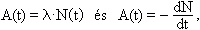
amelyeket egyenlővé téve:
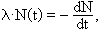
illetve egyszerűbb alakban:
λ·N(t) = −N'(t),
amelyet átrendezve felismerhető, hogy az egyenlet egy állandó együtthatójú elsőrendű lineáris homogén differenciálegyenlet:
N'(t) + λ·N(t) = 0.
Az egyenlet megoldásához az időtől függő tényezőket egy oldalra rendezve:
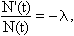
majd mindkét oldalt t szerint integrálva:

valamint átrendezve:
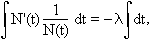
a bal oldal integrálását a helyettesítéssel való integrálás alapösszefüggése alapján, a jobb oldalét a konstans integrálási szabálya alapján elvégezve:
ln N(t) + C = −λt + C,
a konstansokat a jobb oldalra rendezve:
ln N(t) = −λt + C,
majd mindkét oldalt exponenciális függvénnyé alakítva:
eln N(t) = e−λt + C,
amelyet egyszerűsítve és átrendezve adódik az általános megoldás:
N(t) = eC · e−λt.
Az N(t0) = N(0) kezdeti feltételt behelyettesítve:
N(0) = eC · e−λ· 0 = eC · 1,
vagyis:
eC = N(0).
A fentiek alapján a bomlásállandóval kifejezett bomlástörvény:
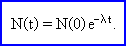
A felezési idővel és a bomlásállandóval kifejezett bomlástörvény csupán az exponenciális tag kitevőjében különbözik. A kitevőket egyenlővé téve:
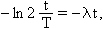
amiből a felezési idő és a bomlásállandó összefüggése:
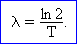
Tudomány és Technika (test@t-es-t.hu)
| Tudomány és Technika | Természettudományok | Atomok és elemek |