Vissza a főoldalra Vissza a Tudományos érdekességek oldalra
|
A π
meghatározása Arkhimédész módszerével (2002.02.20.) |
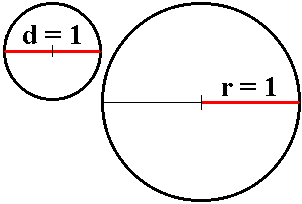
Próbálkozzunk meg a π kiszámításával magunk is! Határozzuk meg az egységnyi átmérőjű kör kerületét és az egységnyi sugarú kör területét! Mi persze már előre tudjuk hogy mind a két eredmény a π lesz.

Mindkét számításnál Arkhimédész módszerét fogjuk alkalmazni, ez ugyanis az elmúlt néhány ezer év alatt már elég jól bevált. Egy kör köré rajzolt egyenlő oldalú érintősokszög, illetve a körbe rajzolt egyenlő oldalú húrsokszög kerülete a sokszög oldalszámának növelésével egyre közelebb kerül a kör kerületéhez. Az alábbi ábrán hatszögekkel van bemutatva a módszer.
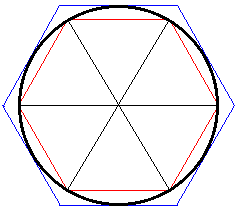
A sokszög felbontható egyenlőszárú egybevágó háromszögekre. A következő ábrán a körbe rajzolt húrsokszög oldalszámának növelésére láthatunk példát.
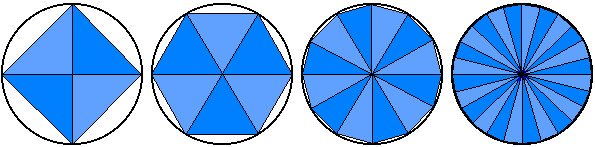
Az egységnyi átmérőjű kör kerülete
Megfigyelhető, hogy a húrsokszög kerülete egyre jobban közelít a kör kerületéhez. A fenti szép ábra ellenére mi mégis az érintősokszög módszerével fogjuk kiszámítani a π-t, a következőképpen:
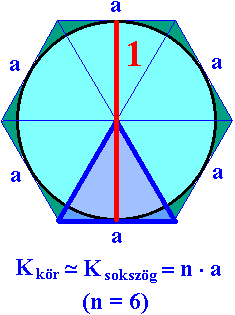
Az ábrán egy egységnyi átmérőjű kör látható, amely köré egy érintősokszög (itt éppen egy hatszög) van rajzolva. A sokszög a fent bejelölt (kék) háromszögekből áll. Bármilyen n oldalszámú sokszöget választunk, az mindig egybevágó egyenlőszárú háromszögekből fog állni; annyiból, ahány oldalú a sokszög. Az ábrából látható, hogy a sokszög kerülete egyenlő az egyenlőszárú háromszögek a alapjainak összegével. Ez az összeg annál jobban megközelíti a kör kerületét, minél nagyobb a sokszög oldalainak száma. Ha tudjuk, hogy hány oldalú a sokszögünk, akkor már csak ki kell számolnunk az a hosszúságot, és azt az oldalak n számával beszorozva, közelítőleg megkapjuk a kör kerületét. Az a hosszúságot a következő ábra alapján határozzuk meg.
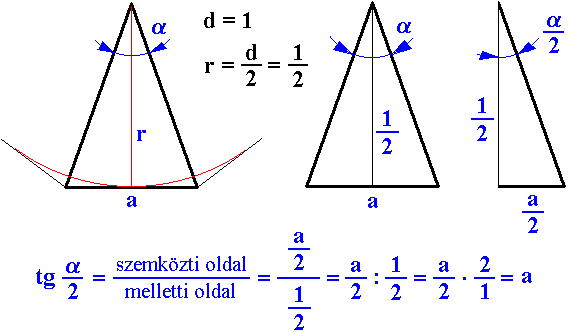
A kör köré rajzolt érintősokszög egyetlen háromszögéből indulunk ki. Látható, hogy az egyenlőszárú háromszög alaphoz tartozó magassága pontosan a kör sugara, tehát ½. Ez a magasságvonal egyben a háromszög szimmetriatengelye is. Számításainkat a háromszög szimmetriatengelyétől jobbra eső derékszögű háromszögön végezzük. Az ábrán látható, hogy az említett háromszög hosszabbik befogója ismert, ½. A háromszög α szögét pedig a sokszög oldalszámának segítségével kiszámíthatjuk. Ugyanis a kör 360°-os szöge egyenlő arányban oszlik meg a sokszöget alkotó háromszögek között. Tehát
α = 360°/n,
ahol n a sokszög oldalainak száma. Az a érték számítási módjának levezetése a fenti ábrán látható a derékszögű háromszögre érvényes tangens függvény használatával. Így tehát:
a = tg(α/2).
Az α értékét behelyettesítve az előző kifejezésbe:
a = tg[(360°/n)/2],
amit egyszerűsítve:
a = tg(180°/n).
Ez alapján tehát számíthatjuk az érintősokszög egyik oldalának hosszát, aminek felhasználásával a kör kerülete:
Kkör = n ˇ a,
azaz:
Kkör = n tg(180°/n).
Ez egy viszonylag egyszerű képlet, így a számítások egy bizonyos n értékig akár zsebszámológéppel is elvégezhetők. Próbáljuk ki eljárásunkat néhány különböző n értékre!
| n - az érintősokszög oldalainak száma | Kkör - a kör kerületének közelítő értéke |
| 100 | 3,1426266043351147818810632528616 |
| 1 000 | 3,1416029890561561260413432901054 |
| 10 000 | 3,1415927569440529197246707719118 |
| 100 000 | 3,1415926546233357948806636356721 |
| 1 000 000 | 3,1415926536001286640227841259626 |
| 10 000 000 | 3,1415926535898965927182443867604 |
| 100 000 000 | 3,1415926535897942720051993932739 |
| 1 000 000 000 | 3,1415926535897932487980689433794 |
| 10 000 000 000 | 3,1415926535897932385659976388805 |
A táblázatban a π-vel egyező számjegyek kék színnel vannak kiemelve. Jól látszik, hogy felülről közelítünk, hiszen bármilyen nagy oldalszámot is választunk, az érintősokszög kerülete mindig valamivel nagyobb a körénél. Megfigyelhetjük, hogy az érintősokszög oldalszámának megtízszerezése körülbelül két tizedesjegynyi pontosságjavulást okoz.
Az egységnyi sugarú kör területe
Itt is a fentihez hasonló módszerrel fogunk eljárni.
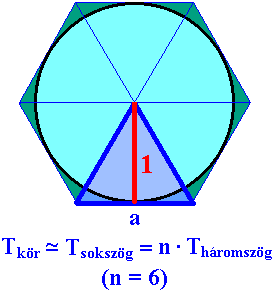
Az ábrán egy egységnyi sugarú kör látható, amely köré egy érintősokszög (itt éppen egy hatszög) van rajzolva. Látható, hogy a sokszög területe egyenlő az egyenlőszárú háromszögek területeinek összegével. Ez az összeg annál jobban megközelíti a kör területét, minél nagyobb a sokszög oldalainak száma. Az egyenlőszárú háromszög területét a következő ábra alapján számítjuk.
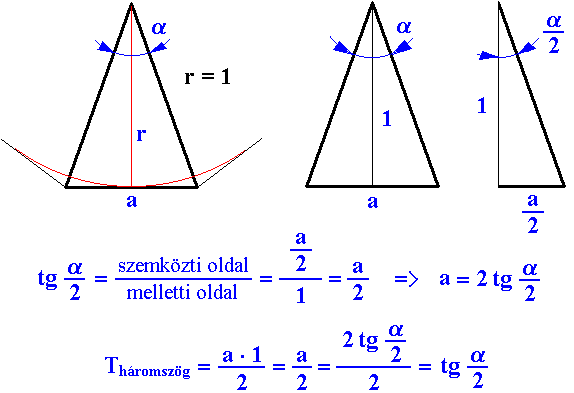
A kör köré rajzolt érintősokszög egyetlen háromszögéből indulunk ki. Látható, hogy az egyenlőszárú háromszög alaphoz tartozó magassága pontosan a kör sugara, tehát 1. Számításainkat a háromszög szimmetriatengelyétől jobbra eső derékszögű háromszögön végezzük. Az ábrán látható, hogy az említett háromszög hosszabbik befogója 1. A háromszög α szögét pedig a sokszög oldalszámának segítségével kiszámíthatjuk:
α = 360°/n,
ahol n a sokszög oldalainak száma. Ezt a kifejezést felhasználva a következőt kapjuk a háromszög területére:
T háromszög = tg(180°/n).
Ennek felhasználásával:
T kör = n ˇ T háromszög ,
amiből:
T kör = n tg(180°/n).
Láthatjuk, hogy eredményünk ugyanaz, mint az előző rész számítási eredménye, tehát az egységnyi átmérőjű kör kerülete és az egységnyi sugarú kör területe számszerűsítve megegyezik.
Meg kell említenünk, hogy számításaink során a tangens függvényt használtuk, amely pontos értékeinek meghatározása szintén nehéz. Így a π pontos értékét csak olyan mélységben számíthatjuk, amíg a pontos tangens érték rendelkezésünkre áll. Például a négyjegyű függvénytáblázat alkalmazásával csak annyit tudhatunk meg a π-ről, hogy értéke 3,2-nél valamivel kevesebb.
Tudomány és Technika (test@t-es-t.hu)